The Reactive Signal Model

Kronos treats all signals the same. An audio sample, a MIDI event and a user interface interaction travel through the signal graph in exactly the same way.

Programs are written as signal flow graphs of high-level abstractions, functions. Functions are composed of other functions. On the lowest level, there are operators that are built into the language core.

During compilation, the program is specialized. All abstraction is collapsed into a static circuit of operators.

At runtime, the Kronos signal model is discrete reactive. Evaluation is carried out by propagating values, one by one, through the circuit. The reactive subsystem controls the relationship between inputs, computation and effects.

Clock Domain Factorization

Music systems tend to be divided in control and audio sections to optimize computational efficiency. This is a form of multirate DSP. Kronos aims to automate multirate factorization as a subset of the reactive semantics.

The factorization is carried out as a global dataflow analysis pass. The basic assumption is that program nodes are referentially transparent. That is, outputs can change only if inputs change.

In terms of discrete updates, the points of time at which an output value changes is the union of those where input values change. As such, inputs to the signal graph can be considered to drive the computation graph. For each signal input, we can derive a minimally sufficient set of program nodes that need to be computed to update the entire circuit, by tracing the dataflow from input downstream.

Memory and Clocks

Multirate factorization, as described above, is obvious when we only deal with referentially transparent operations. As a domain language for signal processing, Kronos provides signal memory as an operator that is referentially transparent at any frozen time point, but variant over time.

Signal processors typically utilize feedback or feedforward delay paths. Kronos utilizes the global dataflow analysis performed for reactive factorization in orded to determine the reference time interval for delays.

For instance, a unit delay operator, z-1, delays the incoming signal by one update frame. If the incoming signal updates at the audio rate, one frame of delay is the inverse of the sampling rate.

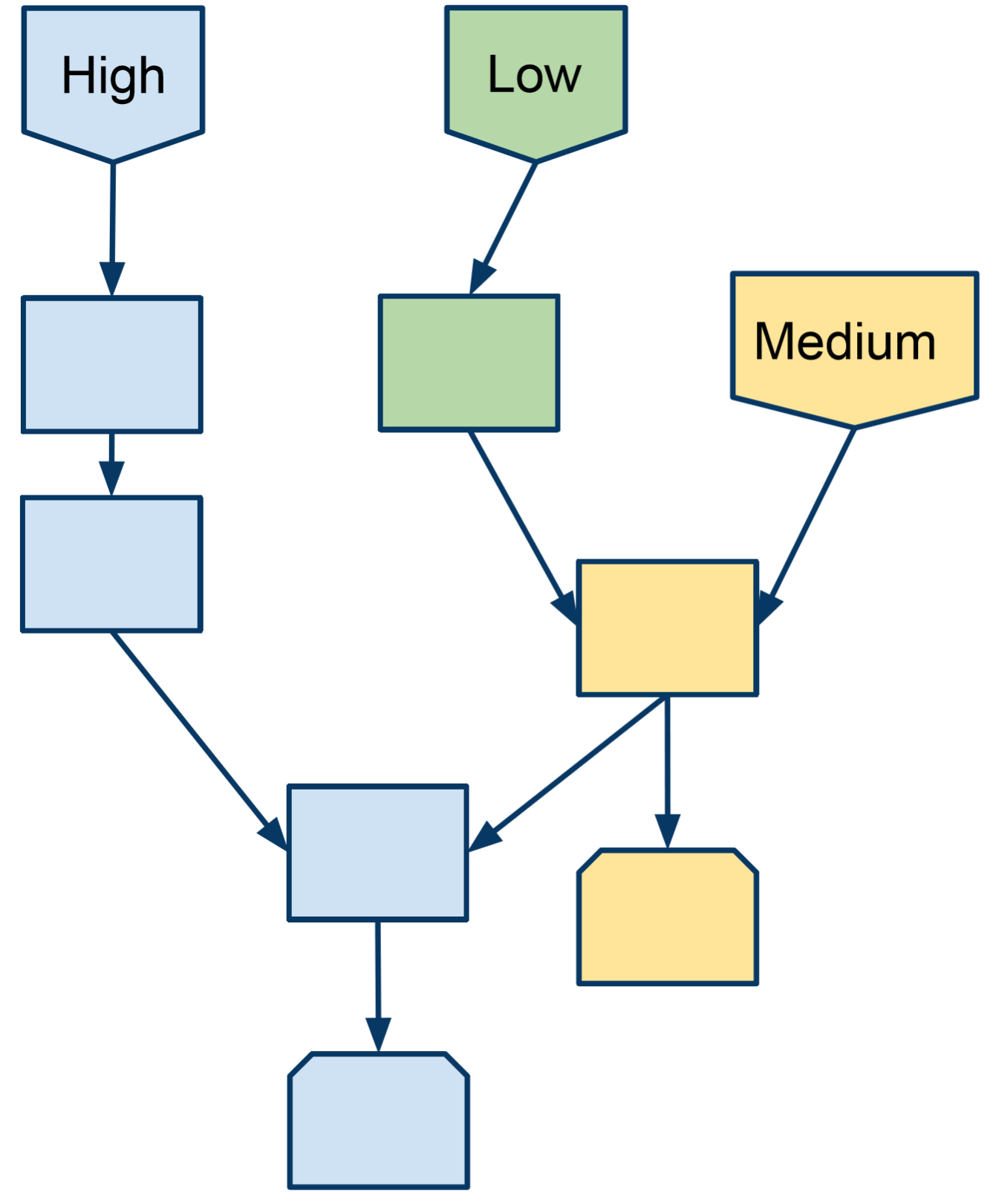
Clock Priority

In signal processing, precise and invariant delay times are important. Consider a simple program that generates an audio rate ramp whose rate of incline is determined by a control input.

rate = Control:Param("rate" 0) st = z-1(Audio:Signal(st) + rate)

According to the logic of dataflow analysis, z-1 sees updates from Audio:Signal as well as Control:Param. Taken as stated, the ramp would increase by an extra tick whenever the rate parameter changes. Usually, the desired behavior is that the audio clock dominates the unit delay.

Kronos signal clocks have a priority, which allows clock domains to dominate each other. By default, audio signals have the highest priority. In the case of equal priorities, a node can belong to multiple clock domains. If the priorities are not equal, the highest priority domain takes over the node and its downstream.

Clock Priority Illustration

Structuring and Destructuring

As a final special case, the priority system is suspended for nodes that perform structuring or destructuring. This allows several distinct rates to coexist in a tuple-valued signal. On destructuring, each tuple element will keep its original rate.

This is also the mechanism that allows functions to accept several parameters with distinct update rates.